You Can't Always Shrink What You Want Paolo Baldan University of Padova Italy PDF version In 2150, Professor Mat, a mathematician, is having hard times in keeping track of the phone numbers of his friends, which, year by year, with the discovery of new inhabited planets, are increasing in cardinality and length. His address book is getting larger and larger, so that he starts seeking for a space saving technique for recording numbers. He explains his problem to Professor Hal, a computer scientist, who replies: "I have an idea. You could represent efficiently a number by means of a program which generates the number itself!  Obviously, this is convenient only if the size of the program is smaller than that of the number..." Mat says: "Ah, I see, this looks nice. I'll think about." The day after they meet again and Mat explains: "Unfortunately the efficient representation you were suggesting cannot be found for any natural number... There are numbers, call them random numbers, for which any program which generates the number have size greater or equal than that of the number itself! Actually, there are infinitely many such numbers!" Q1. Could you justify Professor Mat's statement? I.e., could you prove that there are infinitely many random numbers? Now that Hal is convinced about the infiniteness of the set of random numbers, Mat continues: "Still, you could help me by writing a program that checks whether a number is random or not. Then, before adding a new number in my address book I can check if it is random, and consequently decide whether I should insert directly the number or look for a more efficient program representation." Hal replies: "I am sorry, I can't help you! A program checking whether a number is random or not cannot exist..." Q2. Could you give a proof of Professor Hal's assertion? Note: One can assume that numbers and programs are encoded, as it happens in a computer, as sequences of binary digits. Then by size of a program or number we refer to the length of the corresponding binary encoding. Solutions Q1: Observe that for any n, there are 2n numbers of size n and thus there are numbers of size <= n. 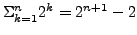Similarly, the number of different programs of size less than n is bounded by the number of different sequences of binary digits of length k < n, i.e., Therefore there are at least 2n numbers of size <= n which cannot be generated by a program of size less than n, and thus which are random. 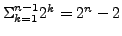As this applies to any n, we deduce that there are infinitely many random numbers. Q2: We proceed by contradiction. Assume that there exists a program Rnd checking whether a number n is random, i.e., Rnd inputs a number n ad returns a value Rnd(n) which is true or false, according to the fact that n is random or not. Using Rnd we can easily construct, for any k, a program GenRnd_k which generates a random number of size larger than k: procedure GenRnd_k {   i=0   while log(i)<=k or not Cas(i) do     i = i + 1   return i } Now, the programs GenRnd_k are essentially all the same apart for the fact that they mention the parameter k. Hence the size of a program GenRnd_k will be log(k) - the size of number k - plus the size C of the common "skeleton" of all programs, i.e., C + log(k) for a suitable fixed constant C. By construction, the number generated by GenRnd_k has size larger than k, which, for a suitable choice of k, is larger than the size C + log(k) of the generating program. Hence the generated number cannot be random. Absurd. Remark 1. The considerations above are sloppy for what concerns the encodings of numbers and programs. If you feel unhappy about that, notice that the arguments can be formalized in a setting in which an Gödel numbering of the computable functions is fixed and a number n is called random if for any index x such that the function is the constant n it holds x > n. Then Q1 can be answered by a combinatorial argument based on the fact that for any computable function there are infinitely many indexes, while a proof of Q2 uses the S-m-n Theorem and Second Recursion Theorem from computability theory. 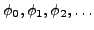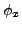Remark 2. This puzzle is inspired by the notion of Kolmogorov-Chaitin complexity in algorithmic information theory and by the related Chaitin's incompleteness theorem (see, e.g., Gregory Chaitin "Information-Theoretic Limitations of Formal Systems". Journal of the ACM 21 (1974), pp. 403-424).